My primary research interests are:
- Numerical Wave Propagation
- Theoretical Acoustics and Seismology
- Applied Statistics, Array Processing, and Inverse Theory
Jordan W. Bishop
Research Projects
Improved infrasound array processing with robust estimators
Abstract
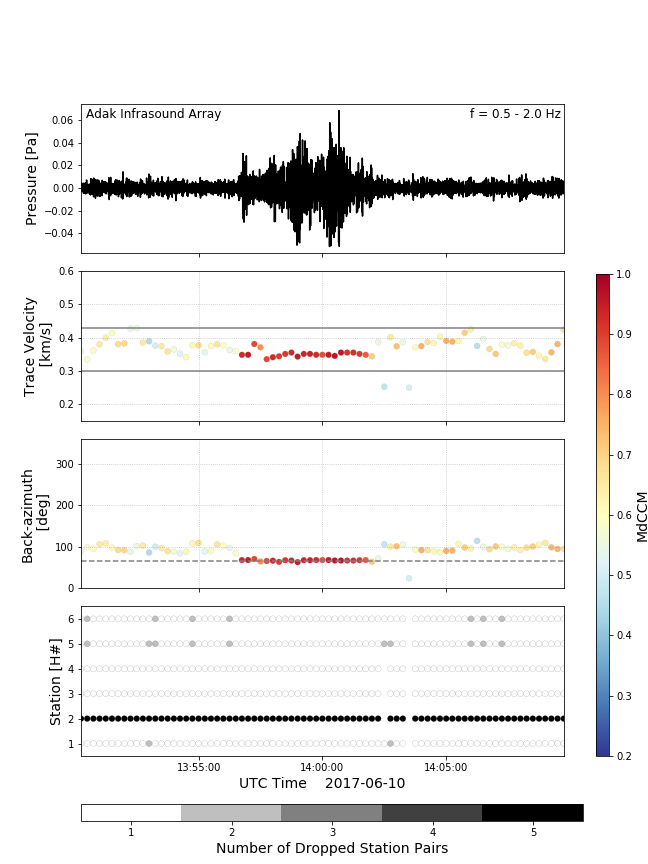Infrasound array data are commonly used to detect and characterize infrasonic signals from a variety of natural and anthropogenic sources. Here we examine the effectiveness of robust regression estimators (L1-norm regression, M-estimators and least trimmed squares) for infrasound array processing, and compare them against standard array processing algorithms (least-squares estimation, frequency–wavenumber analysis and progressive multi-channel correlation) using a combination of real and synthetic data. Of particular interest is how each algorithm performs when one of the array elements produces data outliers. Synthetic tests on elements containing a clock error, constant values or only pink noise are performed, and we analyse the relative ability of the estimators to recover plane wave parameters. The L1-norm regression, M-estimate, frequency–wavenumber analysis and least trimmed squares estimates provided superior results than conventional least-squares estimation. Evaluation of least trimmed squares weights consistently identified the element with the simulated error, providing additional information on array performance. Least trimmed squares processing consistently identified an element with reversed polarity for Alaska Volcano Observatory array ADKI. International Monitoring System stations IS57 and IS55 were likewise processed. Data from an element of IS57, which had lower cross-correlation values than the remaining elements, were consistently identified as having outliers in array processing. An element with a timing error was identified in the analysis of IS55 data. These results suggest robust regression methods, in particular least trimmed squares, improve upon standard methods and should be used more widely, as they can provide robust array processing results and insight into array performance. Further, robust regression methods are not limited to infrasound array processing applications, and it is likely that they would also be effective for seismic array data.
Spectral Element Modeling of Acoustic to Seismic Coupling Over Topography
Abstract
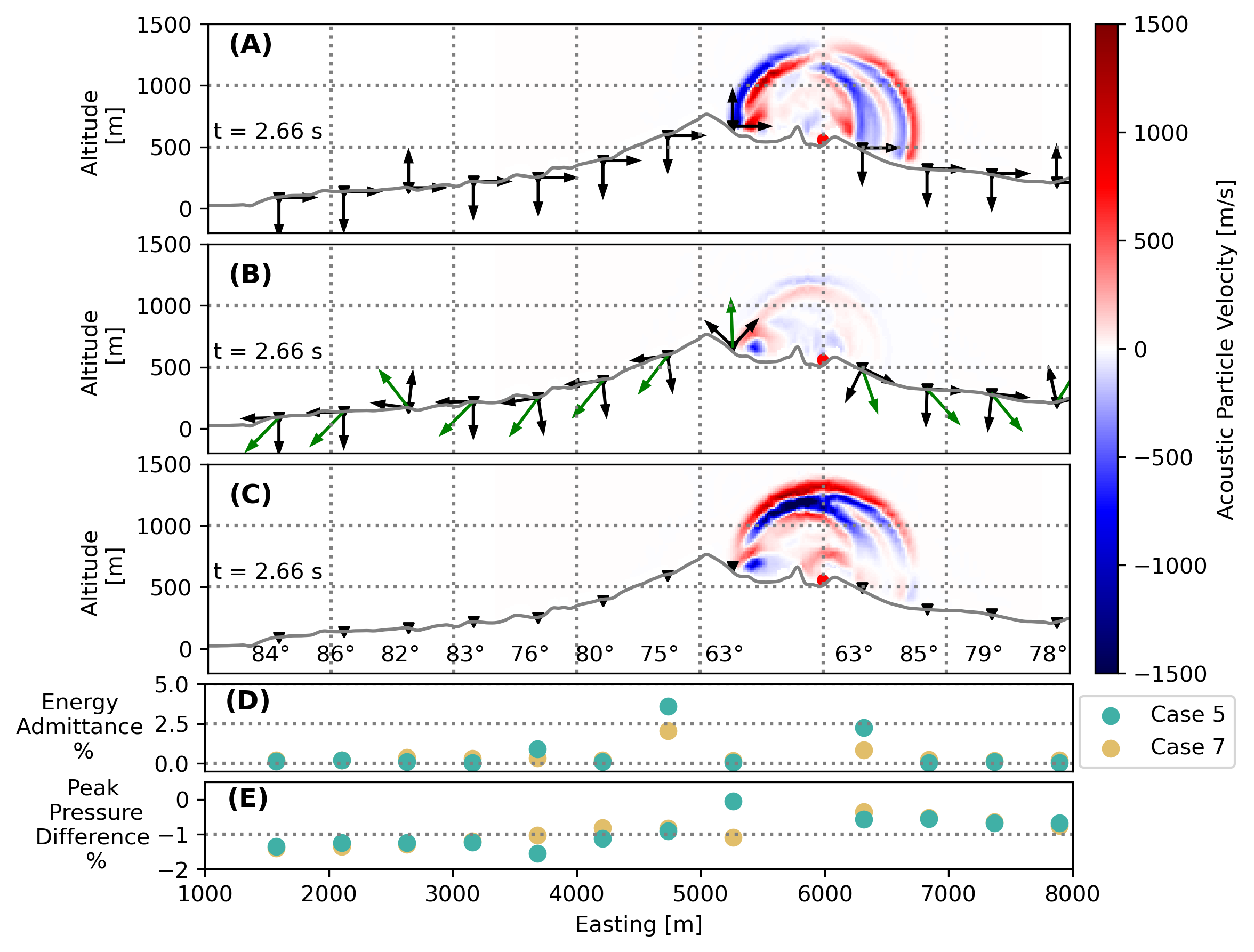Acoustic waves in the atmosphere are commonly recorded on seismometers as they couple into the ground. These signals, here called ground coupled airwaves, are not commonly considered in numerical modeling of infrasound propagation, which often assumes a rigid unmeshed boundary. Starting from an analytically-tractable spherical wave model, we analyze how the coupling of an acoustic wave into a planar elastic halfspace changes over a wide range of scenarios. We use energy admittance to quantify acoustic to seismic coupling over both a planar elastic halfspace and meshed topography. Our spectral element and analytic calculations have different maxima as a function of incidence angle, with very high admittance values for near-vertical incidence (maximum ≈78%). Energy admittance calculations at shallow incidence angles are much smaller (less than 1%). In simulations over the complex topography of Sakurajima Volcano, we attribute the variable spatial pattern of energy admittance to changes in earth parameters between each model. The observed pressure difference over the simulated 15 km region appears to be < 2 %. While this value is relatively small, the cumulative addition over 100s of km and multiple acoustic bounce points may be significant. Acoustic to seismic coupling along the propagation path may bias long distance yield estimates, particularly when infrasound propagates over regions with steep topography or particularly slow seismic velocities, such as alluvial planes.